Формула синуса суммы двух углов. Купить диплом о высшем образовании недорого

Образовательный журнал для школьников, воспитателей и учителей

Тангенс суммы двух углов. Купить диплом о высшем образовании недорого

В курсе тригонометрии, которая охватывает большое количество уроков в 10 классе, изучаются основные четыре тригонометрических функций: синус, косинус, тангенс и котангенс. Школьники должны уметь обращаться с данными функциями, строить их графики, провести анализ каждой из функции, строить графики преобразованных функций, уметь работать с таблицей тригонометрических значений и т.д.

Также, они должны уметь обращаться и воспроизводить некоторые основные формулы тригонометрии, использовать их при решении практических примеров. Это все рассматривалось в предыдущих видеоуроках. Школьники могут просмотреть и освежить материал в своей голове.

Итак, данный видеоурок посвящен изучению формул тангенса суммы и разности аргументов. Ранее изучались формулы синуса суммы и разности аргументов, также косинуса.

Они демонстрируются диктором и выводятся на экран, 0обведенные в красные рамки, для того, чтобы подчеркнуть важность запоминания данных формул.

Что касается тангенса, мы знаем, как можно записать данное понятие, то есть выразить, через синус и косинус. Тангенс суммы аргументов можно записать как деление синуса суммы аргументов на косинус суммы аргументов. Имеем дробь, где числитель и знаменатель можно расписать по изученным заранее формулам. Получаем уже готовую новую формулу, которую можно слега упростить и преобразовать. Диктор предлагает каждый член многочлена поделить на произведение косинуса одного аргумента и синуса иного. Поделив, некоторые члены сократятся, и выражение уменьшится в целом.

Получаем упрощенную новую формулу, которую стоит запомнить. Если понять принцип ее получения, то никаких проблем в дальнейшем понимании и запоминании не появятся.

Далее указывается, что аргументы не могут принимать значения, которые лежат на асимптотах графика функции тангенса. Для сумм аргументов также выводятся исключения. Этот момент учитель обязательно должен рассмотреть с классом.

В первом примере, который выводится в видеоуроке, предлагается вычислить некоторое достаточно большое дробное вырадение, которое и в знаменателе, и в числителе содержит сумму тангенсов. Так как аргументы при тангенсе не являются табличными значениями, рекомендуется привести их в виде суммы более удобных градусов. Проделав данную процедуру можно использовать изученную формулу для дальнейшего решения и получения ответа.

Второй пример предлагает упростить некоторое выражение, которое представляет собой сумму двух дробей. С правой стороны приводятся все выноски, которые используются при решении задачи. Диктор спокойным и понятным голосом объясняет все шаг за шагом. Не пропущен ни один момент.

Третий пример более сложный. Здесь предлагается вычислить тангенс от некоторого значения, если известны некоторые данные. При решении также пользуются ранее изученные формулы, которые появляются в выносках с правой стороны.

Решение достаточное длинное. Выводится в итоге ответ. После этого примера, в видеозаписи рассматривается еще один пример-уравнение. Так как при его решении и используется тригонометрическая таблица значений, она выводится на экран для наглядности и простоты. Таким образом, школьники могут увидеть, откуда взяты те или иные значения, лучше понять.

Подобные примеры можно задать ученикам для выполнения дома. Если у них появятся проблемы при решении, они могу т обратиться к данной видеозаписи и просмотреть еще раз.

Данный электронный ресурс может быть использован для демонстрации в школе во время урока. Учитель сможет «оживить» урок с помощью подобных материалов. Он станет более запоминающимся и интересным. В случае если у школьников появятся вопросы, учитель или репетитор, просматривающий вместе с ним урок, сможет прокомментировать более подробно и объяснить. Сообразительные ученики смогут самостоятельно понять материал и освоить без дополнительной помощи.

Тангенс суммы и разности аргументов

Мы уже познакомились с формулами, которые выражают синус и косинус суммы и разности аргументов. Показать формулы

Рассмотрим, как можно выразить тангенс суммы и разности аргументов. Вспомним, что тангенс, это отношение синуса числа к косинусу этого числа

Тогда тангенс суммы двух углов выразим через синус и косинус суммы двух углов, применяя формулы синус суммы и косинус суммы:

sin(x + y) = sin x cos y + cos x sin y,

cos (x + y) = cos x cos y – sin x sin y.

(ведь, если существуют тангенсы углов х и у, произведение косинусов этих углов отлично от нуля), после деления числителя и знаменателя на cosx cosy получим в числителе сумму а это равно tgx и а это равно tgy.

В знаменателе сокращаем и получаем единицу

как и в числителе а это равно tgxи а это равно tgy.

(Тангенс суммы двух аргументов равен сумме тангенсов этих аргументов, деленной на единицу минус произведение тангенсов этих аргументов.)

Аналогично доказывается формула для тангенса разности аргументов:

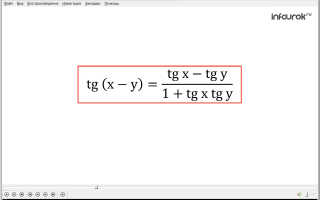
tg(х-у) =. (Тангенс разности двух аргументов равен разности тангенсов этих аргументов, деленной на единицу плюс произведение тангенсов этих аргументов.)

Разумеется, что все тангенсы имеют смысл, т.е. х+ πn, у + πn,

х+у+ πn (для тангенса суммы двух аргументов), х – у+ πn (для тангенса разности двух аргументов).

ПРИМЕР 1. Вычислить.

Решение. Данное выражение представляет собой правую часть формулы тангенс суммы для аргументов 16° и 44°. Следовательно, приведем выражение к виду левой части и получим, что тангенс равен 60 0 , следовательно равен. (Показать таблицу значений)

ПРИМЕР 2. Упростить выражение + (частное суммы тангенсов аргументов икс и игрек на тангенс суммы этих аргументов плюс частное разности тангенсов аргументов икс и игрек на тангенс разности этих аргументов).

Решение. В знаменателе первой и второй дроби применим формулы тангенса суммы и разности аргументов, проведем сокращения и получим 1 – tgxtgy + 1 + tgxtgy , – tgxtgy и tgxtgy в результате дает ноль, тогда в ответе 2.

1 – tgxtgy + 1 + tgxtgy = 2.

ПРИМЕР 3. Вычислить tg(+y) (тангенс пи на четыре плюс игрек), если известно, что cosy = , π

Вывод формулы синус суммы двух углов. Купить диплом о высшем образовании недорого

– уж наверняка встретятся задания по тригонометрии. Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами. На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля .

А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела. Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот. Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.

Будем опираться на следующие формулы:

Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:

Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:

Аналогично получаются и формулы других кратных углов:

Прежде чем двигаться дальше, рассмотрим одну задачу.
Дано: угол – острый.
Найти его косинус, если
Решение, данное одним учеником:
Т.к. , то sin a = 3,а cos a = 4.
(Из математического юмора)

Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin 2 a +cos 2 a = 1 и разделим его на cos 2 a . Получим:

Так что решением этой задачи будет:

(Т.к. угол острый, при извлечении корня берётся знак +)

Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию. Выведем её так:

Сразу выводится и

Из формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла:
cos 2 a = cos 2 a –sin 2 a
прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.
cos 2a +1 = cos 2 a –sin 2 a +cos 2 a +sin 2 a
2cos 2 a = cos 2 a +1
Выражая cos a через cos 2 a и выполняя замену переменных, получаем:

Знак берётся в зависимости от квадранта.

Аналогично, отняв от левой части равенства единицу, а от правой – сумму квадратов синуса и косинуса, получим:
cos 2a -1 = cos 2 a –sin 2 a –cos 2 a –sin 2 a
2sin 2 a = 1-cos 2 a

И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sin a +sin b . Введём переменные x и y такие, что a = x+y, b+x-y. Тогда
sin a +sin b = sin (x+y)+sin (x-y) = sin xcos y+cos xsin y+sin xcos y-cos xsin y = 2sin xcos y. Выразим теперь x и y через a и b.

Поскольку a = x+y, b = x-y, то . Поэтому

Сразу же можно вывести

Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.

Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.

tg alpha cdot ctg alpha = 1

Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.

При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.

Нахождение тангенса и котангенса через синус и косинус

Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению frac=frac , а отношение frac=frac — будет являться котангенсом.

Добавим, что только для таких углов alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg alpha=frac .

Например: tg alpha = frac является справедливой для углов alpha , которые отличны от frac<2>+pi z , а ctg alpha=frac — для угла alpha , отличного от pi z , z — является целым числом.

Зависимость между тангенсом и котангенсом

tg alpha cdot ctg alpha=1

Данное тождество справедливо только для таких углов alpha , которые отличны от frac <2>z . Иначе или котангенс или тангенс не будут определены.

Опираясь на вышеизложенные пункты, получаем, что tg alpha = frac , а ctg alpha=frac . Отсюда следует, что tg alpha cdot ctg alpha = frac cdot frac=1 . Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.

Зависимости между тангенсом и косинусом, котангенсом и синусом

tg^ <2>alpha + 1=frac<1> alpha> — сумма квадрата тангенса угла alpha и 1 , равна обратному квадрату косинуса этого угла. Данное тождество справедливо для всех alpha , отличных от frac<2>+ pi z .

1+ctg^ <2>alpha=frac<1>alpha> — сумма 1 и квадрат котангенса угла alpha , равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого alpha , отличного от pi z .

Примеры с решениями задач на использование тригонометрических тождеств

Пример 1

Найдите sin alpha и tg alpha , если cos alpha=-frac12 и frac <2>> > ; для котангенса > > >

Интегралы

Разложения в ряды

Чтобы получить разложение тангенса по степеням x , нужно взять несколько членов разложения в степенной ряд для функций sin x и cos x и разделить эти многочлены друг на друга , . При этом получаются следующие формулы.

при .
где B n – числа Бернулли. Они определяются либо из рекуррентного соотношения:
;
;
где .
Либо по формуле Лапласа:

Обратные функции

Обратными функциями к тангенсу и котангенсу являются арктангенс и арккотангенс , соответственно.

Арктангенс, arctg

Арккотангенс, arcctg

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.

Самые часто задаваемые вопросы

Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.

Какие виды оплаты вы принимаете? Ответ Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.

Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами? Ответ В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.

Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.

Что делать при обнаружении в документе опечаток и ошибок? Ответ Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.

Что нужно сделать, чтобы заказать диплом в вашей компании? Ответ Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.

Мне нужно было приобрести диплом для устройства на работу по профессии менеджер. И самое главное, что и опыт, и навыки у меня есть, но без документа я не могу, никуда устроится. Попав на ваш сайт, все-таки решился на покупку диплома. Диплом был выполнен за 2 дня!! Теперь у меня есть работа, о которой я раньше и не мечтал!! Спасибо!

Формула для нахождения синуса. Купить диплом о высшем образовании недорого

Косинус суммы и разности двух углов

В этом параграфе будут доказаны следующие две формулы:

cos (α + β) = cos α cos β – sin α sin β, (1)

cos (α – β) = cos α cos β + sin α sin β. (2)

Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов.

Нам удобнее будет начать с доказательства формулы (2). Для простоты изложения предположим сначала, что углы α и β удовлетворяют следующим условиям:

1) каждый из этих углов неотрицателен и меньше 2π :

Пусть положительная часть оси 0х является общей начальной стороной углов α и β .

Конечные стороны этих углов обозначим соответственно через 0А и 0В. Очевидно, что угол α – β можно рассматривать как такой угол, на который нужно повернуть луч 0В вокруг точки 0 против часовой стрелки, чтобы его направление совпало с направлением луча 0А.

На лучах 0А и 0В отметим точки М и N, отстоящие от начала координат 0 на расстоянии 1, так что 0М = 0N = 1.

В системе координат х0у точка М имеет координаты (cos α, sin α ), а точка N – координаты (cos β , sin β ). Поэтому квадрат расстояния между ними равен:

d 1 2 = (cos α – cos β) 2 + (sin α – sin β) 2 = cos 2 α – 2 cos α cos β +

+ cos 2 β + sin 2 α – 2sin α sin β + sin 2 β = .

При вычислениях мы воспользовались тождеством

sin 2 φ + cos 2 φ = 1 .

Теперь рассмотрим другую систему координат В0С, которая получается путем поворота осей 0х и 0у вокруг точки 0 против часовой стрелки на угол β .

В этой системе координат точка М имеет координаты (cos (α – β ), sin (α – β )), а точка N -координаты (1,0). Поэтому квадрат расстояния между ними равен:

d 2 2 = 2 + 2 = cos 2 (α – β) – 2 cos (α – β) + 1 +

Но расстояние между точками М и N не зависит от того, относительно какой системы координат мы рассматриваем эти точки. Поэтому

2 (1 – cos α cos β – sin α sin β) = 2 .

Отсюда и вытекает формула (2).

Теперь следует вспомнить о тех двух ограничениях, которые мы наложили для простоты изложения на углы α и β .

Требование, чтобы каждый из углов α и β был неотрицательным, на самом деле не существенно. Ведь к любому из этих углов можно прибавить угол, кратный 2я, что никак не отразится на справедливости формулы (2). Точно так же от каждого из данных углов можно вычесть угол, кратный 2π . Поэтому можно считать, что β . Действительно, если α α ; поэтому, учитывая четность функции cos х , получаем:

cos (α – β) = cos (β – α) = cos β cos α + sin β sin α,

что по существу совпадает с формулой (2). Таким образом, формула

cos (α – β) = cos α cos β + sin α sin β

верна для любых углов α и β . В частности, заменяя в ней β на –β и учитывая, что функция cos х является четной, а функция sin х нечетной, получаем:

cos (α + β) = cos [α – (- β)] =cos α cos (-β) + sin α sin (-β) =

= cos α cos β – sin α sin β,

что доказывает формулу (1).

Итак, формулы (1) и (2) доказаны.

1) cos 75° = cos (30° + 45°) = cos 30° cos 45°-sin 30°-sin 45° =

2) cos 15° = cos (45° – 30°) = cos 45° cos 30° + sin 45° sin 30° =

1 . Вычислить, не пользуясь тригонометрическими таблицами:

a) cos 17° cos 43° – sin 17° sin 43°;

б) sin 3° sin 42° – cos 39° cos 42°;

в) cos 29° cos 74° + sin 29° sin 74°;

г) sin 97° sin 37° + cos 37° cos 97°;

д) cos 3π / 8 cos π / 8 + sin 3π / 8 sin π / 8 ;

e) sin 3π / 5 sin 7π / 5 – cos 3π / 5 cos 7π / 5 .

a). cos (α + π / 3 ) + cos (π / 3 – α ) .

б). cos (36° + α ) cos (24° – α ) + sin (36° + α ) sin (α – 24°).

в). sin (π / 4 – α ) sin (π / 4 + α ) – cos (π / 4 + α ) cos (π / 4 – α )

a) cos (α – β) , если

cos α = – 2 / 5 , sin β = – 5 / 13 ;

Источники:

https://www.chalt-1school.ru/literature/tangens-summy-dvuh-uglov-kupit-diplom-o-vysshem-obrazovanii-nedorogo/
https://drivemc.ru/vyvod-formuly-sinus-summy-dvuh-uglov-kupit-diplom-o-vysshem-obrazovanii/
https://moesms.ru/formula-dlya-nahozhdeniya-sinusa-kupit-diplom-o-vysshem-obrazovanii-nedorogo.html