Как начертить фигуру не отрывая руки. Построение фигур одним росчерком карандаша

Построение фигур одним росчерком карандаша

I. Постановка проблемной ситуации.

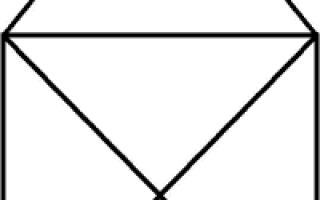
Наверное, все помнят с детства, что очень популярна была следующая задача: не отрывая карандаша от бумаги и не проводя по одной линии дважды, начертить “открытый конверт”:

Попробуйте нарисовать “открытый конверт”.
Как вы видите, что у некоторых получается, а у некоторых нет. Почему это происходит? Как правильно рисовать, чтобы получилось? И для чего она нужна? Чтобы ответить на эти вопросы, я расскажу вам, один исторический факт.

Город Кенигсберг (после мировой войны он называется Калининград) стоит на реке Преголь. Некогда там было 7 мостов, которые связывали между собой берега и два острова. Жители города заметили, что они никак не могут совершить прогулку по всем семи мостам, пройдя по каждому из них ровно один раз. Так возникла головоломка: “можно ли пройти все семь кенигсбергских мостов ровно один раз и вернуться в исходное место?”.

Попробуйте и вы, может у кого-нибудь получится.

В 1735 году эта задача стала известна Леонарду Эйлеру. Эйлер выяснил, что такого пути нет, т. е. доказал, что эта задача неразрешима. Конечно, Эйлер решил не только задачу о кенигсбергский мостах, а целый класс аналогичных задач, для которых разработал метод решения. Можно заметить, что задача состоит в том, чтобы по карте провести маршрут – линию, не отрывая карандаша от бумаги, обойти все семь мостов и вернуться в начальную точку. Поэтому Эйлер стал рассматривать вместо карты мостов схему из точек и линий, отбросив мосты, острова и берега, как не математические понятия. Вот что у него получилось:

А, В – острова, M, N – берега, а семь кривых – семь мостов.

Теперь задача такая – обойти контур на рисунке так, чтобы каждая кривая проводилась ровно один раз.
В наше время такие схемы из точек и линий стали называть графами, точки называют вершинами графа, а линии – ребрами графа. В каждой вершине графа сходится несколько линий. Если число линий четно, то вершина называется четная, если число вершин нечетно, то вершина называется нечетной.

Докажем неразрешимость нашей задачи.
Как видим, в нашем графе все вершины нечетные. Для начала докажем, что, если обход графа начинается не с нечетной точки, то он обязательно должен закончится в этой точке

Рассмотрим для примера вершину с тремя линиями. Если мы по одной линии пришли, по другой вышли, и по третьей опять вернулись. Все дальше идти некуда ( ребер больше нет). В нашей задаче мы сказали, что все точки нечетные, значит, выйдя из одной из них, мы должны закончить сразу в трех остальных нечетных точках, чего не может быть.
До Эйлера ни кому в голову не приходило, что головоломка о мостах и другие головоломки с обходом контура, имеет отношение к математике. Анализ Эйлера таких задач “является первым ростком новой области математики, сегодня известной под названием топология”.

Топология – это раздел математики, изучающий такие свойства фигур, которые не меняются при деформациях, производимых без разрывов и склеивания.
Например, с точки зрения топологии, круг, эллипс, квадрат и треугольник обладают одинаковыми свойствами и являются одной и той же фигурой, так как можно деформировать одну в другую, а вот кольцо к ним не относится, так как, чтобы его деформировать в круг, необходима склейка.

II. Признаки вычерчивания графа.

1. Если в графе нет нечетных точек, то ее можно нарисовать одним росчерком, не отрывая карандаша от бумаги, начиная с любого места.
2. Если в графе две нечетные вершины, то ее можно начертить одним росчерком, не отрывая карандаша от бумаги, причем вычерчивать нужно начинать в одной нечетной точке, а закончить в другой.
3. Если в графе более двух нечетных точек, то ее нельзя начертить одним росчерком карандаша.

Вернемся к нашей задаче с открытым конвертом. Подсчитаем количество четных и нечетных точек: 2 нечетные и 3 четные, значит, эту фигуру можно начертить одним росчерком, причем начать нужно в нечетной точке. Попробуйте, теперь у всех получилось?

Закрепим полученные знания. Определите, какие фигуры можно построить, а какие нельзя.

а) Все точки четные, поэтому эту фигуру можно построить, начиная с любого места, например:

б) В этой фигуре две нечетные точки, поэтому ее можно построить не отрывая, карандаша от бумаги, начиная с нечетной точки.
в) В этой фигуре четыре нечетные точки, поэтому ее нельзя построить.
г) Здесь все точки четные, поэтому ее можно построить, начиная с любого места.

Проверим, как вы усвоили новые знания.

III. Самостоятельная работа по карточкам с индивидуальными заданиями.

Задание: проверить, можно ли совершить прогулку по всем мостам, пройдя по каждому из них ровно один раз. И если можно, то нарисовать путь.

Как нарисовать фигуру не отрывая руки. Построение фигур одним росчерком карандаша

I. Постановка проблемной ситуации.

Наверное, все помнят с детства, что очень популярна была следующая задача: не отрывая карандаша от бумаги и не проводя по одной линии дважды, начертить “открытый конверт”:

Попробуйте нарисовать “открытый конверт”.
Как вы видите, что у некоторых получается, а у некоторых нет. Почему это происходит? Как правильно рисовать, чтобы получилось? И для чего она нужна? Чтобы ответить на эти вопросы, я расскажу вам, один исторический факт.

Город Кенигсберг (после мировой войны он называется Калининград) стоит на реке Преголь. Некогда там было 7 мостов, которые связывали между собой берега и два острова. Жители города заметили, что они никак не могут совершить прогулку по всем семи мостам, пройдя по каждому из них ровно один раз. Так возникла головоломка: “можно ли пройти все семь кенигсбергских мостов ровно один раз и вернуться в исходное место?”.

Попробуйте и вы, может у кого-нибудь получится.

В 1735 году эта задача стала известна Леонарду Эйлеру. Эйлер выяснил, что такого пути нет, т. е. доказал, что эта задача неразрешима. Конечно, Эйлер решил не только задачу о кенигсбергский мостах, а целый класс аналогичных задач, для которых разработал метод решения. Можно заметить, что задача состоит в том, чтобы по карте провести маршрут – линию, не отрывая карандаша от бумаги, обойти все семь мостов и вернуться в начальную точку. Поэтому Эйлер стал рассматривать вместо карты мостов схему из точек и линий, отбросив мосты, острова и берега, как не математические понятия. Вот что у него получилось:

А, В – острова, M, N – берега, а семь кривых – семь мостов.

Теперь задача такая – обойти контур на рисунке так, чтобы каждая кривая проводилась ровно один раз.
В наше время такие схемы из точек и линий стали называть графами, точки называют вершинами графа, а линии – ребрами графа. В каждой вершине графа сходится несколько линий. Если число линий четно, то вершина называется четная, если число вершин нечетно, то вершина называется нечетной.

Докажем неразрешимость нашей задачи.
Как видим, в нашем графе все вершины нечетные. Для начала докажем, что, если обход графа начинается не с нечетной точки, то он обязательно должен закончится в этой точке

Рассмотрим для примера вершину с тремя линиями. Если мы по одной линии пришли, по другой вышли, и по третьей опять вернулись. Все дальше идти некуда (ребер больше нет). В нашей задаче мы сказали, что все точки нечетные, значит, выйдя из одной из них, мы должны закончить сразу в трех остальных нечетных точках, чего не может быть.
До Эйлера ни кому в голову не приходило, что головоломка о мостах и другие головоломки с обходом контура, имеет отношение к математике. Анализ Эйлера таких задач “является первым ростком новой области математики, сегодня известной под названием топология”.

Топология – это раздел математики, изучающий такие свойства фигур, которые не меняются при деформациях, производимых без разрывов и склеивания.
Например, с точки зрения топологии, круг, эллипс, квадрат и треугольник обладают одинаковыми свойствами и являются одной и той же фигурой, так как можно деформировать одну в другую, а вот кольцо к ним не относится, так как, чтобы его деформировать в круг, необходима склейка.

II. Признаки вычерчивания графа.

1. Если в графе нет нечетных точек, то ее можно нарисовать одним росчерком, не отрывая карандаша от бумаги, начиная с любого места.
2. Если в графе две нечетные вершины, то ее можно начертить одним росчерком, не отрывая карандаша от бумаги, причем вычерчивать нужно начинать в одной нечетной точке, а закончить в другой.
3. Если в графе более двух нечетных точек, то ее нельзя начертить одним росчерком карандаша.

Вернемся к нашей задаче с открытым конвертом. Подсчитаем количество четных и нечетных точек: 2 нечетные и 3 четные, значит, эту фигуру можно начертить одним росчерком, причем начать нужно в нечетной точке. Попробуйте, теперь у всех получилось?

Закрепим полученные знания. Определите, какие фигуры можно построить, а какие нельзя.

а) Все точки четные, поэтому эту фигуру можно построить, начиная с любого места, например:

б) В этой фигуре две нечетные точки, поэтому ее можно построить не отрывая, карандаша от бумаги, начиная с нечетной точки.
в) В этой фигуре четыре нечетные точки, поэтому ее нельзя построить.
г) Здесь все точки четные, поэтому ее можно построить, начиная с любого места.

Проверим, как вы усвоили новые знания.

III. Самостоятельная работа по карточкам с индивидуальными заданиями.

Задание : проверить, можно ли совершить прогулку по всем мостам, пройдя по каждому из них ровно один раз. И если можно, то нарисовать путь.

IV. Итоги занятия.

Предполагается, что заданная фигура состоит из точек, соединенных прямыми или искривленными отрезками. Следовательно, в каждой такой точке сходится определенное отрезков. Такие фигуры принято называть графами.

Если в точке сходится четное число отрезков, то и саму такую точку называют четной вершиной. Если число отрезков нечетное, то вершина называется нечетной. Например, квадрат, в котором проведены обе , обладает четырьмя нечетными вершинами и одной четной – в точке пересечения диагоналей.

У отрезка по определению два , и следовательно, он всегда соединяет две вершины. Поэтому, просуммировав все входящие отрезки для всех вершин графа, можно только четное число. Следовательно, каков бы ни был граф, нечетных вершин в нем всегда будет четное количество (в том ноль).

Граф, в котором вовсе нет нечетных вершин, всегда можно начертить, не отрывая руки от бумаги. При этом все равно, с какой вершины начинать.

Если нечетных вершин всего две, то такой граф тоже уникурсален. Путь обязательно должен начинаться в одной из нечетных вершин, а закончиться – в другой из них.

Фигура, в которой нечетных вершин четыре или больше, не уникурсальна, и без повторений линий начертить ее не . Например, тот же квадрат с проведенными диагоналями не уникурсален, так как у него четыре нечетных вершины. Но квадрат с одной диагональю или «конверт» – квадрат с диагоналями и «крышечкой» – можно начертить одной линией.

Чтобы решить задачу, нужно представить, что каждая проведенная линия исчезает из фигуры – второй раз по ней пройти нельзя. Следовательно, изображая уникурсальную фигуру, нужно следить, чтобы оставшаяся часть работы не распадалась на не связанные между собой части. Если случится, довести дело до конца уже не получится.

• Как нарисовать не отрывая руки закрытый конверт?

Квадрат – это равносторонний и прямоугольный четырехугольник. Его нарисовать очень просто. Начните тренировку сначала на тетради в клетку. С помощью простого карандаша и невидимого квадрата из научитесь рисовать квадрат не отрывая руку от бумаги.

• – простой карандаш;
• – листок в клетку;
• – лист А4;
• – линейка.

Можно попробовать так: без использования линейки и точек. Изобразите квадрат посредине листа. Сначала не старайтесь нарисовать его четырьмя идеальными линиями. Чертите стороны квадрата «навылет», наводя дополнительные линии, пока квадрат не получится квадратом. При этом не отрывайте руку от бумаги. Проводите линии параллельно краям бумаги. Сделайте несколько таких тренировочных упражнений. Этот научит вас ровные линии и квадрат не отрывая руки .

В нарисованных городских или сельских пейзажах нередко фигурируют различные мосты . Эта особенная постройка может выглядеть изящной и невесомой, а может, наоборот, создавать впечатление строгого и тяжелого сооружения.

Равновеликие и равносоставленные фигуры

С равными фигурами не следует смешивать равновеликие и равносоставленные фигуры – при всей близости данных понятий.
Равновеликими называются такие фигуры, которые имеют равную площадь, если это фигуры на плоскости, или равный объем, если речь идет о трехмерны телах. Совпадение всех элементов, составляющих данные фигуры, не является обязательным. Равные фигуры будут равновеликими всегда, но не всякие равновеликие фигуры можно назвать равными.

Понятие равносоставленности чаще всего применяют к многоугольникам. Оно подразумевает, что многоугольники можно разбить на одинаковое количество соответственно равных фигур. Равносоставленные многоугольники всегда являются равновеликими.

Современных детей сложно чем-то увлечь. Они любят смотреть мультики и играть в компьютерные игры. Но умные родители всегда способны заинтересовать свое чадо. Например, они могут предложить ему найти способ, как нарисовать конверт не отрывая руки. О некоторых хитростях этого задания читайте ниже.

Разминка

Прежде чем начать мучить ребенка логическими заданиями, нужно провести с ним подготовительную работу. Зачем она нужна? Чтобы ребенок не мухлевал, когда начнет ломать голову над вопросом о том, как нарисовать конверт не отрывая руки. Ведь самое интересное в этой задачке то, что линия должна идти от точки к точке беспрерывно.

Какие же задания можно предложить ребенку в качестве разминки? Конечно, первое это должны быть восьмерки. Рисование этой цифры и стресс снимает, и мозг очищает, и руку тренирует. В общем, полезное упражнение. После этого можно переходить к рисованию округлых форм. Это могут быть завитки или любые другие закорючки, главное, чтобы в процессе рисования ребенок не отрывал карандаша и изображал все одной плавной линией.

Как нарисовать закрытый конверт

Многие родители и сами потратили не один час, прежде чем предложить такое задание ребенку. Вы тоже можете попробовать. Но мы сразу можем вас огорчить – выполнить такое задание, немного не слукавив, просто невозможно. Поэтому расскажем способ, который поможет вам и вашему ребенку немного выйти за рамки обычной логики, чтобы понять, как нарисовать закрытый конверт не отрывая руки.

Берем лист бумаги и загибаем у него край. Отгибаем его назад. Теперь наша задача состоит в том, чтобы нарисовать верхний край закрытого конверта как раз на линии загиба. Чтобы легче было понимать, расставим точки на концах прямоугольника. Пронумеруем их, начиная с верхнего левого угла. Здесь будет стоять цифра один и дальше по часовой стрелке. Из цифры 4 к 1 проводим линию, теперь соединяем 1 с 2 и теперь рисуем диагональ к 4. От 4 к 3 ведем прямую линию, а потом опять диагональ к 1.

Теперь переходим к самому интересному. Загибаем край нашего листа и изображаем зигзаг, который образует как бы шапку нашего конверта. Проходить она будет из 1 к 2. Осталось соединить 2 и 3 прямой линией – и головоломка решена. Отгибаем часть листа назад. Загадку, как нарисовать конверт не отрывая руки, можно предлагать не только детям, но и друзьям или коллегам.

Как нарисовать открытый конверт

Те, кто внимательно читали предыдущий пункт и по описанию создал свой рисунок, уже поняли, как ответить на вопрос, поставленный выше. Ведь решение загадки, как нарисовать открытый конверт не отрывая руки, будет аналогичным написанному в предыдущем пункте. Только здесь не придется загибать и отгибать части листа. Все изображение будет делаться одной линией по той же схеме.

Но если вы не хотите повторяться, то мы предлагаем еще один способ, который приведет к тому же результату. Как нарисовать конверт не отрывая руки вторым способом? Для начала рисуем опять точками прямоугольник и снова его нумеруем, как в предыдущем пункте. Из цифры 4 к 2 ведем диагональ, от 2 к 3 – прямую линию, а от 3 к 1 – опять диагональ. Дальше нужно нарисовать уголок. От 1 к 2 рисуем зигзаг, который обозначает верхнюю часть конверта. От 2 возвращаемся к 1 прямой линией и завершаем наше построение поочередно проводя прямые от 1 к 4 и от 4 к 3.

Зачем нужны такие задачки

Такие нужно выполнять не только детям, но и взрослым. Благодаря им человеческий мозг напрягается и начинает работать. Если приучить себя выполнять по аналогичному заданию каждый день, уже через месяц можно будет заметить, что в критических ситуациях решения генерируется быстрее и сил на это затрачивается меньше. Школьникам особенно полезно изучать задачки на логику. Таким образом они тренируют креативность и учатся нестандартно подходить к стандартным вопросам.

Как начертить не отрывая руки. Построение фигур одним росчерком карандаша

Предполагается, что заданная фигура состоит из точек, соединенных прямыми или искривленными отрезками. Следовательно, в каждой такой точке сходится определенное отрезков. Такие фигуры принято называть графами.

Если в точке сходится четное число отрезков, то и саму такую точку называют четной вершиной. Если число отрезков нечетное, то вершина называется нечетной. Например, квадрат, в котором проведены обе , обладает четырьмя нечетными вершинами и одной четной – в точке пересечения диагоналей.

У отрезка по определению два , и следовательно, он всегда соединяет две вершины. Поэтому, просуммировав все входящие отрезки для всех вершин графа, можно только четное число. Следовательно, каков бы ни был граф, нечетных вершин в нем всегда будет четное количество (в том ноль).

Граф, в котором вовсе нет нечетных вершин, всегда можно начертить, не отрывая руки от бумаги. При этом все равно, с какой вершины начинать.

Если нечетных вершин всего две, то такой граф тоже уникурсален. Путь обязательно должен начинаться в одной из нечетных вершин, а закончиться – в другой из них.

Фигура, в которой нечетных вершин четыре или больше, не уникурсальна, и без повторений линий начертить ее не . Например, тот же квадрат с проведенными диагоналями не уникурсален, так как у него четыре нечетных вершины. Но квадрат с одной диагональю или «конверт» – квадрат с диагоналями и «крышечкой» – можно начертить одной линией.

Чтобы решить задачу, нужно представить, что каждая проведенная линия исчезает из фигуры – второй раз по ней пройти нельзя. Следовательно, изображая уникурсальную фигуру, нужно следить, чтобы оставшаяся часть работы не распадалась на не связанные между собой части. Если случится, довести дело до конца уже не получится.

• Как нарисовать не отрывая руки закрытый конверт?

Квадрат – это равносторонний и прямоугольный четырехугольник. Его нарисовать очень просто. Начните тренировку сначала на тетради в клетку. С помощью простого карандаша и невидимого квадрата из научитесь рисовать квадрат не отрывая руку от бумаги.

• – простой карандаш;
• – листок в клетку;
• – лист А4;
• – линейка.

Можно попробовать так: без использования линейки и точек. Изобразите квадрат посредине листа. Сначала не старайтесь нарисовать его четырьмя идеальными линиями. Чертите стороны квадрата «навылет», наводя дополнительные линии, пока квадрат не получится квадратом. При этом не отрывайте руку от бумаги. Проводите линии параллельно краям бумаги. Сделайте несколько таких тренировочных упражнений. Этот научит вас ровные линии и квадрат не отрывая руки .

В нарисованных городских или сельских пейзажах нередко фигурируют различные мосты . Эта особенная постройка может выглядеть изящной и невесомой, а может, наоборот, создавать впечатление строгого и тяжелого сооружения.

Равновеликие и равносоставленные фигуры

С равными фигурами не следует смешивать равновеликие и равносоставленные фигуры – при всей близости данных понятий.
Равновеликими называются такие фигуры, которые имеют равную площадь, если это фигуры на плоскости, или равный объем, если речь идет о трехмерны телах. Совпадение всех элементов, составляющих данные фигуры, не является обязательным. Равные фигуры будут равновеликими всегда, но не всякие равновеликие фигуры можно назвать равными.

Понятие равносоставленности чаще всего применяют к многоугольникам. Оно подразумевает, что многоугольники можно разбить на одинаковое количество соответственно равных фигур. Равносоставленные многоугольники всегда являются равновеликими.

Современных детей сложно чем-то увлечь. Они любят смотреть мультики и играть в компьютерные игры. Но умные родители всегда способны заинтересовать свое чадо. Например, они могут предложить ему найти способ, как нарисовать конверт не отрывая руки. О некоторых хитростях этого задания читайте ниже.

Разминка

Прежде чем начать мучить ребенка логическими заданиями, нужно провести с ним подготовительную работу. Зачем она нужна? Чтобы ребенок не мухлевал, когда начнет ломать голову над вопросом о том, как нарисовать конверт не отрывая руки. Ведь самое интересное в этой задачке то, что линия должна идти от точки к точке беспрерывно.

Какие же задания можно предложить ребенку в качестве разминки? Конечно, первое это должны быть восьмерки. Рисование этой цифры и стресс снимает, и мозг очищает, и руку тренирует. В общем, полезное упражнение. После этого можно переходить к рисованию округлых форм. Это могут быть завитки или любые другие закорючки, главное, чтобы в процессе рисования ребенок не отрывал карандаша и изображал все одной плавной линией.

Как нарисовать закрытый конверт

Многие родители и сами потратили не один час, прежде чем предложить такое задание ребенку. Вы тоже можете попробовать. Но мы сразу можем вас огорчить – выполнить такое задание, немного не слукавив, просто невозможно. Поэтому расскажем способ, который поможет вам и вашему ребенку немного выйти за рамки обычной логики, чтобы понять, как нарисовать закрытый конверт не отрывая руки.

Берем лист бумаги и загибаем у него край. Отгибаем его назад. Теперь наша задача состоит в том, чтобы нарисовать верхний край закрытого конверта как раз на линии загиба. Чтобы легче было понимать, расставим точки на концах прямоугольника. Пронумеруем их, начиная с верхнего левого угла. Здесь будет стоять цифра один и дальше по часовой стрелке. Из цифры 4 к 1 проводим линию, теперь соединяем 1 с 2 и теперь рисуем диагональ к 4. От 4 к 3 ведем прямую линию, а потом опять диагональ к 1.

Теперь переходим к самому интересному. Загибаем край нашего листа и изображаем зигзаг, который образует как бы шапку нашего конверта. Проходить она будет из 1 к 2. Осталось соединить 2 и 3 прямой линией – и головоломка решена. Отгибаем часть листа назад. Загадку, как нарисовать конверт не отрывая руки, можно предлагать не только детям, но и друзьям или коллегам.

Как нарисовать открытый конверт

Те, кто внимательно читали предыдущий пункт и по описанию создал свой рисунок, уже поняли, как ответить на вопрос, поставленный выше. Ведь решение загадки, как нарисовать открытый конверт не отрывая руки, будет аналогичным написанному в предыдущем пункте. Только здесь не придется загибать и отгибать части листа. Все изображение будет делаться одной линией по той же схеме.

Но если вы не хотите повторяться, то мы предлагаем еще один способ, который приведет к тому же результату. Как нарисовать конверт не отрывая руки вторым способом? Для начала рисуем опять точками прямоугольник и снова его нумеруем, как в предыдущем пункте. Из цифры 4 к 2 ведем диагональ, от 2 к 3 – прямую линию, а от 3 к 1 – опять диагональ. Дальше нужно нарисовать уголок. От 1 к 2 рисуем зигзаг, который обозначает верхнюю часть конверта. От 2 возвращаемся к 1 прямой линией и завершаем наше построение поочередно проводя прямые от 1 к 4 и от 4 к 3.

Зачем нужны такие задачки

Такие нужно выполнять не только детям, но и взрослым. Благодаря им человеческий мозг напрягается и начинает работать. Если приучить себя выполнять по аналогичному заданию каждый день, уже через месяц можно будет заметить, что в критических ситуациях решения генерируется быстрее и сил на это затрачивается меньше. Школьникам особенно полезно изучать задачки на логику. Таким образом они тренируют креативность и учатся нестандартно подходить к стандартным вопросам.

I. Постановка проблемной ситуации.

Наверное, все помнят с детства, что очень популярна была следующая задача: не отрывая карандаша от бумаги и не проводя по одной линии дважды, начертить “открытый конверт”:

Попробуйте нарисовать “открытый конверт”.
Как вы видите, что у некоторых получается, а у некоторых нет. Почему это происходит? Как правильно рисовать, чтобы получилось? И для чего она нужна? Чтобы ответить на эти вопросы, я расскажу вам, один исторический факт.

Город Кенигсберг (после мировой войны он называется Калининград) стоит на реке Преголь. Некогда там было 7 мостов, которые связывали между собой берега и два острова. Жители города заметили, что они никак не могут совершить прогулку по всем семи мостам, пройдя по каждому из них ровно один раз. Так возникла головоломка: “можно ли пройти все семь кенигсбергских мостов ровно один раз и вернуться в исходное место?”.

Попробуйте и вы, может у кого-нибудь получится.

В 1735 году эта задача стала известна Леонарду Эйлеру. Эйлер выяснил, что такого пути нет, т. е. доказал, что эта задача неразрешима. Конечно, Эйлер решил не только задачу о кенигсбергский мостах, а целый класс аналогичных задач, для которых разработал метод решения. Можно заметить, что задача состоит в том, чтобы по карте провести маршрут – линию, не отрывая карандаша от бумаги, обойти все семь мостов и вернуться в начальную точку. Поэтому Эйлер стал рассматривать вместо карты мостов схему из точек и линий, отбросив мосты, острова и берега, как не математические понятия. Вот что у него получилось:

А, В – острова, M, N – берега, а семь кривых – семь мостов.

Теперь задача такая – обойти контур на рисунке так, чтобы каждая кривая проводилась ровно один раз.
В наше время такие схемы из точек и линий стали называть графами, точки называют вершинами графа, а линии – ребрами графа. В каждой вершине графа сходится несколько линий. Если число линий четно, то вершина называется четная, если число вершин нечетно, то вершина называется нечетной.

Докажем неразрешимость нашей задачи.
Как видим, в нашем графе все вершины нечетные. Для начала докажем, что, если обход графа начинается не с нечетной точки, то он обязательно должен закончится в этой точке

Рассмотрим для примера вершину с тремя линиями. Если мы по одной линии пришли, по другой вышли, и по третьей опять вернулись. Все дальше идти некуда (ребер больше нет). В нашей задаче мы сказали, что все точки нечетные, значит, выйдя из одной из них, мы должны закончить сразу в трех остальных нечетных точках, чего не может быть.
До Эйлера ни кому в голову не приходило, что головоломка о мостах и другие головоломки с обходом контура, имеет отношение к математике. Анализ Эйлера таких задач “является первым ростком новой области математики, сегодня известной под названием топология”.

Топология – это раздел математики, изучающий такие свойства фигур, которые не меняются при деформациях, производимых без разрывов и склеивания.
Например, с точки зрения топологии, круг, эллипс, квадрат и треугольник обладают одинаковыми свойствами и являются одной и той же фигурой, так как можно деформировать одну в другую, а вот кольцо к ним не относится, так как, чтобы его деформировать в круг, необходима склейка.

II. Признаки вычерчивания графа.

1. Если в графе нет нечетных точек, то ее можно нарисовать одним росчерком, не отрывая карандаша от бумаги, начиная с любого места.
2. Если в графе две нечетные вершины, то ее можно начертить одним росчерком, не отрывая карандаша от бумаги, причем вычерчивать нужно начинать в одной нечетной точке, а закончить в другой.
3. Если в графе более двух нечетных точек, то ее нельзя начертить одним росчерком карандаша.

Вернемся к нашей задаче с открытым конвертом. Подсчитаем количество четных и нечетных точек: 2 нечетные и 3 четные, значит, эту фигуру можно начертить одним росчерком, причем начать нужно в нечетной точке. Попробуйте, теперь у всех получилось?

Закрепим полученные знания. Определите, какие фигуры можно построить, а какие нельзя.

а) Все точки четные, поэтому эту фигуру можно построить, начиная с любого места, например:

б) В этой фигуре две нечетные точки, поэтому ее можно построить не отрывая, карандаша от бумаги, начиная с нечетной точки.
в) В этой фигуре четыре нечетные точки, поэтому ее нельзя построить.
г) Здесь все точки четные, поэтому ее можно построить, начиная с любого места.

Проверим, как вы усвоили новые знания.

III. Самостоятельная работа по карточкам с индивидуальными заданиями.

Задание : проверить, можно ли совершить прогулку по всем мостам, пройдя по каждому из них ровно один раз. И если можно, то нарисовать путь.

Источники:

https://urok.1sept.ru/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/101844/
https://diveles.ru/kak-narisovat-figuru-ne-otryvaya-ruki-postroenie-figur-odnim-roscherkom.html
https://mode-house.ru/kak-nachertit-ne-otryvaya-ruki-postroenie-figur-odnim/