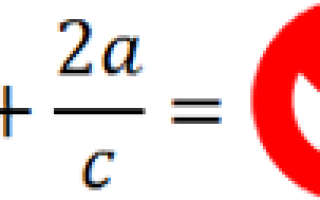Скобках дроби разными знаменателями. Составление системы уравнений

Сложение и вычитание алгебраических дробей

Алгебраические дроби складывают и вычитают по правилам сложения и вычитания обыкновенных дробей.

Сложение алгебраических дробей

Складывать можно только дроби с одинаковыми знаменателями!

Нельзя складывать дроби без преобразований

Можно складывать дроби

При сложении алгебраических дробей с одинаковыми знаменателями:

1. числитель первой дроби складывается с числителем второй дроби;
2. знаменатель остаётся прежним.

Рассмотрим пример сложения алгебраических дробей.

Так как знаменатель у обеих дробей « 2а », значит, дроби можно сложить.

Сложим числитель первой дроби с числителем второй дроби, а знаменатель оставим прежним. При сложении дробей в полученном числителе приведем подобные.

Вычитание алгебраических дробей

Вычитать можно только дроби с одинаковыми знаменателями!

При вычитании алгебраических дробей с одинаковыми знаменателями:

1. из числителя первой дроби вычитается числитель второй дроби.
2. знаменатель остаётся прежним.

Обязательно заключите в скобки весь числитель вычитаемой дроби.

Иначе вы сделаете ошибку в знаках при раскрытии скобок вычитаемой дроби.

Рассмотрим пример вычитания алгебраических дробей.

Так как у обеих алгебраических дробей знаменатель « 2с », значит, эти дроби можно вычитать.

Вычтем из числителя первой дроби « (a + d) » числитель второй дроби « (a − b) ». Не забудем заключить числитель вычитаемой дроби в скобки. При раскрытии скобок используем правило раскрытия скобок.

Приведение алгебраических дробей к общему знаменателю

Рассмотрим другой пример. Требуется сложить алгебраические дроби.

В таком виде сложить дроби нельзя, так как у них разные знаменатели.

Прежде чем складывать алгебраические дроби их необходимо привести к общему знаменателю.

Правила приведения алгебраических дробей к общему знаменателю очень похожи на правила приведения к общему знаменателю обыкновенных дробей. .

В итоге мы должны получить многочлен, который без остатка разделится на каждый прежний знаменатель дробей.

Чтобы привести алгебраические дроби к общему знаменателю необходимо сделать следующее.

1. Работаем с числовыми коэффициентами. Определяем НОК (наименьшее общее кратное) для всех числовых коэффициентов.
2. Работаем с многочленами. Определяем все различные многочлены в наибольших степенях.
3. Произведение числового коэффициента и всех различных многочленов в наибольших степенях и будет общим знаменателем.
4. Определяем, на что нужно умножить каждую алгебраическую дробь, чтобы получить общий знаменатель.

Вернемся к нашему примеру.

Рассмотрим знаменатели « 15a » и « 3 » обеих дробей и найдем для них общий знаменатель.

1. Работаем с числовыми коэффициентами. Находим НОК (наименьшее общее кратное — это число, которое без остатка делится на каждый числовый коэффициент). Для « 15 » и « 3 » — это « 15 ».
2. Работаем с многочленами. Необходимо перечислить все многочлены в наибольших степенях. В знаменателях « 15a » и « 5 » есть только
   один одночлен — « а ».
3. Перемножим НОК из п.1 « 15 » и одночлен « а » из п.2. У нас получится « 15a ». Это и будет общим знаменателем.
4. Для каждой дроби зададим себе вопрос: «На что нужно умножить знаменатель этой дроби, чтобы получить « 15a »?».

Рассмотрим первую дробь. В этой дроби и так знаменатель « 15a », значит, ее не требуется ни на что умножать.

Рассмотрим вторую дробь. Зададим вопрос: «На что нужно умножить « 3 », чтобы получить « 15a »?» Ответ — на « 5a ».

При приведении к общему знаменателю дроби умножаем на « 5a » и числитель, и знаменатель .

Сокращенную запись приведения алгебраической дроби к общему знаменателю можно записать через «домики» .

Для этого держим в уме общий знаменатель. Над каждой дробью сверху «в домике» пишем, на что умножаем каждую из дробей.

Теперь, когда у дробей одинаковые знаменатели, дроби можно сложить.

Рассмотрим пример вычитания дробей с разными знаменателями.

В таком виде вычитать дроби нельзя, так как у них разные знаменатели. Чтобы вычесть дроби, необходимо привести их к общему знаменателю.

Рассмотрим знаменатели « (x − y) » и « (x + y) » обеих дробей и найдем для них общий знаменатель.

1. Работаем с числовыми коэффициентами. Числовых коэффициентов в знаменателях нет, поэтому переходим к многочленам.
2. Работаем с многочленами. Находим все различные многочлены из знаменателей в наибольших степенях и перемножаем их.

Многочлены необходимо рассматривать целиком! Для удобства заключайте целый многочлен в скобки.

У нас есть два различных многочлена в знаменателях « (x − y) » и « (x + y) ». Их произведение будет общим знаменателем, т.е. « (x − y)(x + y) » — общий знаменатель.

Теперь дроби можно вычитать, т.к. у них одинаковый знаменатель.

Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения

В некоторых примерах, чтобы привести алгебраические дроби к общему знаменателю, нужно использовать формулы сокращенного умножения.

Рассмотрим пример сложения алгебраических дробей, где нам потребуется использовать формулу разности квадратов.

В первой алгебраической дроби знаменатель « (p 2 − 36) ». Очевидно, что к нему можно применить формулу разности квадратов.

После разложения многочлена « (p 2 − 36) » на произведение многочленов
« (p + 6)(p − 6) » видно, что в дробях повторяется многочлен « (p + 6) ». Значит, общим знаменателем дробей будет произведение многочленов « (p + 6)(p − 6) ».

Прежде чем приводить многочлены к общему знаменателю, попытайтесь использовать формулы сокращённого умножения или вынесение общего множителя за скобки.

Примеры сложения и вычитания дробей с разными знаменателями с использованием формул сокращенного умножения.

Сложение и вычитание алгебраических дробей с вынесением общего множителя за скобки

На первый взгляд одинаковых многочленов в обеих дробях нет.

Вынесем общий множитель « а » за скобки в обоих знаменателях.

После вынесения общего множителя « а » за скобки, в обоих знаменателях появился одинаковый одночлен « а ». Значит, общий знаменатель для обеих дробей будет выглядеть так: « а(а + 1)(b + 1) ».

Сложение алгебраической дроби с одночленом или числом

Рассмотрим пример. Требуется сложить алгебраическую дробь с одночленом (буквой).

Чтобы сложить одночлен или число с алгебраической дробью, нужно представить одночлен в виде дроби со знаменателем « 1 ».

Представим одночлен « а » как алгебраическую дробь со знаменателем « 1 ».

Подобное действие можно сделать, так как при делении на единицу получается тот же самый одночлен.

Теперь приведем алгебраические дроби к общему знаменателю « (а − 1) » и решим пример.

Скобках дроби разными знаменателями. Составление системы уравнений

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.

Вычитание дробей с одинаковыми знаменателями, примеры:

,

,

Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.

Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.

Правила вычитания дробей – правильной из целого числа (натурального числа) :

• Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
• Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
• Выполняем обратное преобразование, то есть избавляемся от неправильной дроби – выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.

Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .

Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.

Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!

Порядок действий при вычитании дробей с разными знаменателями.

• найти НОК для всех знаменателей;
• поставить для всех дробей дополнительные множители;
• умножить все числители на дополнительный множитель;
• полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
• произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.

Первый вариант вычитания смешанных дробей.

Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Второй вариант вычитания смешанных дробей.

Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3

Как решать уравнения с дробями. Показательное решение уравнений с дробями.

Решение уравнений с дробями рассмотрим на примерах. Примеры простые и показательные. С их помощью вы наиболее понятным образом сможете усвоить, как решать уравнения с дробями.
Например, требуется решить простое уравнение x/b + c = d.

Уравнения такого типа называется линейным, т.к. в знаменателе находятся только числа.

Решение выполняется путем умножения обоих частей уравнения на b, тогда уравнение принимает вид x = b*(d – c), т.е. знаменатель дроби в левой части сокращается.

Например, как решить дробное уравнение:
x/5+4=9
Умножаем обе части на 5. Получаем:
х+20=45
x=45-20=25

Другой пример, когда неизвестное находится в знаменателе:

Уравнения такого типа называются дробно-рациональными или просто дробными.

Решать дробное уравнение бы будем путем избавления от дробей, после чего это уравнение, чаще всего, превращается в линейное или квадратное, которое решается обычным способом. Следует только учесть следующие моменты:

• значение переменной, обращающее в 0 знаменатель, корнем быть не может;
• нельзя делить или умножать уравнение на выражение =0.

Здесь вступает в силу такое понятие, как область допустимых значений (ОДЗ) – это такие значения корней уравнения, при которых уравнение имеет смысл.

Таким образом решая уравнение, необходимо найти корни, после чего проверить их на соответствие ОДЗ. Те корни, которые не соответствуют нашей ОДЗ, из ответа исключаются.

Например, требуется решить дробное уравнение:

Исходя из вышеуказанного правила х не может быть = 0, т.е. ОДЗ в данном случае: х – любое значение, отличное от нуля.

Избавляемся от знаменателя путем умножения всех членов уравнения на х

И решаем обычное уравнение

5x – 2х = 1
3x = 1
х = 1/3

Решим уравнение посложнее:

Здесь также присутствует ОДЗ: х -2.

Решая это уравнение, мы не станем переносить все в одну сторону и приводить дроби к общему знаменателю. Мы сразу умножим обе части уравнения на выражение, которое сократит сразу все знаменатели.

Для сокращения знаменателей требуется левую часть умножить на х+2, а правую – на 2. Значит, обе части уравнения надо умножать на 2(х+2):

Это самое обычное умножение дробей, которое мы уже рассмотрели выше

Запишем это же уравнение, но несколько по-другому

Левая часть сокращается на (х+2), а правая на 2. После сокращения получаем обычное линейное уравнение:

х = 4 – 2 = 2, что соответствует нашей ОДЗ

Для закрепления материала рекомендуем еще посмотреть видео.

Решение уравнений с дробями не так сложно, как может показаться. В этой статье мы на примерах это показали. Если у вас возникли какие то трудности с тем, как решать уравнения с дробями, то отписывайтесь в комментариях.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Источники:

https://math-prosto.ru/?page=pages/algebraic_fractions/addition_and_subtraction_algebraic_fractions.php
https://altbasket.ru/skobkah-drobi-raznymi-znamenatelyami-sostavlenie-sistemy-uravnenii/
https://reshit.ru/Kak-reshat-uravneniya-s-drobyami