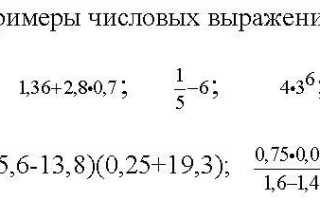Какие выражения являются суммами разностями. Что такое числовые выражения

Числовые выражения

Запись, которая состоит из чисел, знаков и скобок, а также имеет смысл, называется числовым выражением.

Например, следующие записи:

будут являться числовыми выражениями. Следует понимать, что одно число тоже будет являться числовым выражением. В нашем примере, это число 13.

А, например, следующие записи

не будут являться числовыми выражениями, так как они лишены смысла и являются просто набором чисел и знаков.

Значение числового выражения

Так как в качестве знаков в числовых выражениях входят знаки арифметических действий, то мы можем посчитать значение числового выражения. Для этого необходимо выполнить указанные действия.

(100-32)/17 = 4, то есть для выражения (100-32)/17 значением этого числового выражения будет являться число 4.

2*4+7=15, число 15 будет являться значением числового выражения 2*4+7.

Часто для краткости записи не пишут полностью значение числового выражения, а пишут просто “значение выражения”, опуская при этом слово «числового».

Числовое равенство

Если два числовых выражения записаны через знак равно, то эти выражения образуют числовое равенство. Например, выражение 2*4+7=15 является числовым равенством.

Как уже отмечалось выше, в числовых выражениях могут использоваться скобки. Как уже известно скобки влияют на порядок действий.

Вообще, все действия разделены на несколько ступеней.

• Действия первой ступени: сложение и вычитание.
• Действия второй ступени: умножение и деление.
• Действия третей ступени – возведение в квадрат и возведение в куб.

Правила при вычислении значений числовых выражений

При вычислении значений числовых выражений следуют руководствоваться следующими правилами.

• 1. Если выражение не имеет скобок, то надо выполнять действия начиная с высших ступеней: третья ступень, вторая ступень и первая ступень. Если имеется несколько действий одной ступени, то их выполняют в порядке в котором они записаны, то есть слева на право.
• 2. Если в выражении присутствуют скобки, то сначала выполняются действия в скобках, а лишь затем все стальные действия в обычном порядке. При выполнении действий в скобках, если их там несколько, следует пользоваться порядком описанным в пункте 1.
• 3. Если выражение представляет собой дробь, то сначала вычисляются значении в числителе и знаменателе, а потом числитель делится на знаменатель.
• 4. Если в выражении присутствуют вложенные скобки, то выполнять действия следует с внутренних скобок.

Числовые выражения

Числовое выражение – это любая запись из чисел, знаков арифметических действий и скобок. Числовое выражение может состоять и просто из одного числа. Напомним, что основными арифметическими действиями являются «сложение», «вычитание», «умножение» и «деление». Этим действиям соответствуют знаки «+», «-», «∙», «:».

Конечно же, чтобы у нас получилось числовое выражение, запись из чисел и арифметических знаков должна быть осмысленной. Так, например, такую запись 5 : + ∙ нельзя назвать числовым выражением, так как это случайный набор символов, не имеющий смысла. Напротив, 5 + 8 ∙ 9 – уже настоящее числовое выражение.

Значение числового выражения.

Сразу скажем, что если мы выполним действия указанные в числовом выражении, то в результате мы получим число. Это число называется значением числового выражения.

Попробуем вычислить, что у нас получится в результате выполнения действий нашего примера. Согласно порядку выполнения арифметических действий, сначала выполним операцию умножения. Умножим 8 на 9. Получим 72. Теперь сложим 72 и 5. Получим 77.
Итак, 77 – значение числового выражения 5 + 8 ∙ 9.

Числовое равенство.

Можно это записать таким образом: 5 + 8 ∙ 9 = 77. Здесь мы впервые использовали знак «=» («Равно»). Такая запись, при которой два числовых выражения разделены знаком «=», называется числовым равенством. При этом, если значения левой и правой части равенства совпадают, то равенство называют верным. 5 + 8 ∙ 9 = 77 – верное равенство.
Если же мы напишем 5 + 8 ∙ 9 = 100, то это уже будет неверное равенство, так как значения левой и правой части данного равенства уже не совпадают.

Следует отметить, что в числовом выражении мы также можем использовать скобки. Скобки влияют на порядок выполнения действий. Так, например, видоизменим наш пример, добавив скобки: (5 + 8) ∙ 9. Теперь сначала нужно сложить 5 и 8. Получим 13. А затем умножить 13 на 9. Получим 117. Таким образом, (5 + 8) ∙ 9 = 117.
117 – значение числового выражения (5 + 8 ) ∙ 9.

Как прочитать числовое выражение?

Чтобы правильно прочитать выражение, нужно определить какое именно действие выполняется последним для вычисления значения данного числового выражения. Так, если последнее действие вычитание, то выражение называют «разностью». Соответственно, если последнее действие сумма – «суммой», деление – «частным», умножение – «произведением», возведение в степень – «степенью».

Например, числовое выражение (1+5)(10-3) читается так: «произведение суммы чисел 1 и 5 на разность чисел 10 и 3».

Примеры числовых выражений.

Приведем пример более сложного числового выражения:

В данном числовом выражении используются простые числа, обыкновенные и десятичные дроби. Также используются знаки сложения, вычитания, умножения и деления. Черта дроби также заменяет знак деления. При кажущейся сложности, найти значение данного числового выражения довольно просто. Главное уметь выполнять операции с дробями, а также внимательно и аккуратно делать вычисления, соблюдая порядок выполнения действий.

В скобках у нас выражение $frac<1><4>+3,75$ . Преобразуем десятичную дробь 3,75 в обыкновенную.

Далее, в числителе дроби [frac<1,25+3,47+4,75-1,47><4centerdot 0,5>] у нас выражение 1,25+3,47+4,75-1,47. Для упрощения данного выражения применим переместительный закон сложения, который гласит: «От перемены мест слагаемых сумма не изменяется». То есть, 1,25+3,47+4,75-1,47=1,25+4,75+3,47-1,47=6+2=8.

В знаменателе дроби выражение $4centerdot 0,5=4centerdot frac<1><2>=4:2=2$

Когда числовые выражения не имеют смысла?

Рассмотрим еще один пример. В знаменателе дроби $frac<5+5><3centerdot 3-9>$ значением выражения $3centerdot 3-9$ является 0. А, как мы знаем, деление на нуль невозможно. Следовательно, у дроби $frac<5+5><3centerdot 3-9>$ нет значения. Про числовые выражения, у которых нет значения, говорят, что они «не имеют смысла».

Если мы в числовом выражении помимо чисел будем использовать буквы, то у нас получится уже алгебраическое выражение.

Урок по математике в начальной школе “Числовые выражения”, 2-й класс

Разделы: Математика

Класс: 2

В формировании многих качеств, необходимых успешному современному человеку, может большую роль сыграть школьная дисциплина – математика. На уроках математики школьники учатся рассуждать, доказывать, находить рациональные пути выполнения заданий, делать соответствующие выводы. Общепризнанно, что «математика – самый короткий путь к самостоятельному мышлению», «математика ум в порядок приводит» как отмечал М.В. Ломоносов.

Деятельностный подход был разработан в трудах Алексея Николаевича Леонтьева, Даниила Борисовича Эльконина, Петра Яковлевича Гальперина, Александра Владимировича Запорожца в середине 20 века.

Педагогическая практика показывает, что формирование универсальных учебных действий, то есть действий, обеспечивающих умение учиться, самостоятельно искать, находить и усваивать знание – самый прогрессивный путь организации обучения.

Основу концепции деятельностного подхода к обучению составляет положение: усвоение содержания обучения и развитие ученика происходит в процессе его собственной деятельности.

Любое усвоение знаний строится на усвоении учеником учебных действий, овладев которыми, ученик смог бы усваивать знания самостоятельно, пользуясь различными источниками информации. Научить учиться (усваивать информацию) – главный тезис деятельностного подхода.

Цель: познакомить с понятием «числовое выражение», учить говорить на математическом языке.

Задачи:

• учить распознавать числовые выражения, правильно их читать, находить их значения;
• развивать логическое мышление, умение анализировать, делать выводы, развивать речь детей;
• воспитывать самостоятельность, упорство в достижении цели.

I. Оргмомент

– Сегодня у нас не совсем обычный урок. На уроке присутствуют гости. Повернитесь и поздоровайтесь с нашими гостями.
– Повернитесь ко мне.

С добрым утром начат день.
Первым делом гоним лень.
На уроке не зевать,
А работать и считать!

– Ребята, а что вы уже умеете делать? (Ответы детей) Что уже знаете?
(На доске карточки с названием тем: «Во сколько раз больше или меньше?» «Умножение и деление. Часть числа.» «Решение задач на уменьшение и увеличение в несколько раз» «Нахождение числа по нескольким долям» «Нахождение нескольких долей числа» «Название чисел в записях действий»)
– Начинаем урок математики.

II. Актуализация знаний

– На прошлом уроке математики вы учились читать разные примеры, используя названия компонентов и результата действия.
– Прочитайте по-разному примеры на доске: 8 + 2 (появляется карточка: «слагаемое + слагаемое = сумма»)

8 – 2 (уменьшаемое – вычитаемое = разность)
8 * 2 (первый множитель • второй множитель = произведение)
8 : 2 (делимое : делитель = частное)

III. Постановка проблемы

25 + 4 33 + а в – 7 6 • 8 с • 5 (15 – 7) + 4 18 : 3 • 6 – 3

– Разделите записи на карточках на две группы. (Ученик у доски делит записи на группы) (Рассматриваются несколько вариантов группировки)
– Какая запись оказалась лишней?
– Почему?
– Дайте общее название группе. А как ещё можно назвать эти записи? (Выражения))
– Я предлагаю сыграть в игру «Как вы думаете?». Мне нужны две пары.
Каждая пара получает лист – игровое поле и набор карточек. (Играют на доске)

4 > 40
7 = 7
x + 5 > 8
13 – 9
(16 – 9) • 2
63 : 9

– Карточки, на которых, по вашему мнению, записаны числовые выражения, положите на сектор «числовые выражения». Уверены, что на карточке не числовые выражения – сектор «нет», сомневаетесь – сектор «?».
(Выполняют)
– Как вы думаете, правильно или неправильно ребята выполнили задание?
– Как бы вы определили тему нашего урока?
– Чему будем учиться на уроке?
– Откройте учебник на странице 68.
– Прочитайте тему урока вверху страницы.
– Рассмотрите страницу учебника и подумайте, о чём вы хотели бы меня спросить по этой теме?
(На доске карточки-помощницы: Что…? Почему…? Зачем…?)
(Если вопросов нет: «Наверное, вопросы у вас появятся потом»)

IV. «Открытие» нового знания

– Что вы видите на стр. 68? (Таблицу)
– Прочитайте названия столбиков в таблице.
– Это четыре вопроса, в которых нам надо разобраться.
– Что общего во всех записях 1-й колонки?
– Из чего состоит 1-я запись? (Из двух цифр, и знака «+» между числами)
– Что они обозначают? (Числа)
(Аналогично рассматривается запись 2, 3 и 4)
– Что общего? Что в числовом выражении очень важно?(Состоят из чисел)

На доске: 1. Числа
– Какие числа в первой записи? (во 2-й, 3-й, 4-й)

На доске: 1. Числа 5;4
6;7
15;8
48;6
– Что ещё есть в записи кроме чисел? (Знаки действий)

– Какой знак в первой записи? (второй, третьей, четвёртой)

На доске: 1. Числа 5;4
6;7
15;8
48;6
2. знаки действий +
•
–
:
– Работайте в парах: составьте новые числовые выражения, используя те же числа и знаки действий. Докажите.
(Работа в парах. Проверка.)
– Как называется вторая колонка? (Название выражения)
– У каждого выражения есть имя. Кто догадался, как определить название выражения?
– Поработайте в паре: обсудите, какое выражение мы будем называть суммой? Произведением? Разностью? Частным? (Обсуждение)
– Какое выражение мы будем называть суммой? (Выражение, в котором числа соединены знаком « + ») (Аналогично остальные)
На доске: 1. Числа 5; 4
6; 7
15; 8
48; 6
2. знаки действий + – сумма
• – произведение
– – разность
: – частное
– Прочитайте выражения.
– Как называется 3-й столбик? (Вычисление)
– О чём рассказывает этот столбик? (Что с выражением можно выполнить действия (вычислить, найти ответ, сосчитать), решить)
– Можно выполнить действия, вычисления с любым выражением.
– Всю ли таблицу рассмотрели?
– Как называется четвёртый столбик? (Значение выражения)
– Кто догадался, что такое значение выражения? Как бы вы объяснили, что такое значение выражения? (Это число)
– Какое число?
– Как вы понимаете задание «вычислить значение выражения»? (Выполнить вычисления, найти результат, число)
На доске: 1. Числа 5; 4
6; 7
15; 8
48; 6
2. знаки действий + – сумма
• – произведение
– – разность
: – частное
есть значение выражения (его можно найти)
– Что же вы можете рассказать о выражении?

Физминутка

Мы немножко отдохнём.
Встанем, глубоко вздохнём.
Руки в стороны, вперёд.
Дети по лесу гуляли,
За природой наблюдали.
Вверх на солнце посмотрели –
И их всех лучи согрели.
Чудеса у нас на свете:
Стали карликами дети.
А потом все дружно встали,
Великанами мы стали.
Дружно хлопаем,
Ногами топаем!
Хорошо мы погуляли
И немножечко устали!

– Числа в выражении имеют своё название, а значение выражения не имеет?
– Это справедливо?
– Посмотрите на стр. 68 учебника. О чём вели разговор Волк и Заяц?
– Оказывается, название выражения и его значение называются одинаково.
– Чему учились?

V. Комментирование решения типовых задач

– Потренируемся в применении наших знаний.
– Откройте тетрадь на стр. 41 № 129.
– Как будем рассуждать, является ли эта запись выражением?
(Карточка пооперационного контроля:

Источники:

https://www.nado5.ru/e-book/chislovye-vyrazheniya
https://nashol.com/2014083079722/chislovie-virajeniya.html
https://urok.1sept.ru/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/580286/