Треугольная пирамида рисунок как чертить. Завершающий этап выполнения макета

Узнать ещё

Знание — сила. Познавательная информация

Рисунок правильной пирамиды

Чертеж — первый и очень важный шаг в решении геометрической задачи. Каким должен быть рисунок правильной пирамиды?

Сначала вспомним свойства параллельного проектирования:

— параллельные отрезки фигуры изображаются параллельными отрезками;

— сохраняется отношение длин отрезков параллельных прямых и отрезков одной прямой.

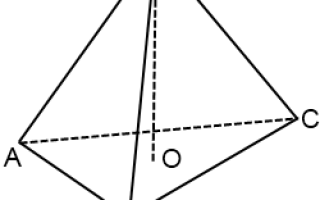
Рисунок правильной треугольной пирамиды

Сначала изображаем основание. Поскольку при параллельном проектировании углы и отношения длин не параллельных отрезков не сохраняются, правильный треугольник в основании пирамиды изображается произвольным треугольником.

Центр правильного треугольника — точка пересечения медиан треугольника. Поскольку медианы в точке пересечения делятся в отношении 2:1, считая от вершины, мысленно соединяем вершину основания с серединой противолежащей стороны, приблизительно делим ее на три части, и на расстоянии 2 частей от вершины ставим точку. Из этой точки вверх проводим перпендикуляр. Это — высота пирамиды. Перпендикуляр рисуем такой длины, чтобы боковое ребро не закрывало изображение высоты.

Рисунок правильной четырехугольной пирамиды

Рисунок правильной четырехугольной пирамиды также начинаем с основания. Поскольку параллельность отрезков сохраняется, а величины углов — нет, то квадрат в основании изображается параллелограммом. Желательно острый угол этого параллелограмма делать поменьше, тогда боковые грани получаются больше. Центр квадрата — точка пересечения его диагоналей. Проводим диагонали, из точки пересечения восстанавливаем перпендикуляр. Этот перпендикуляр — высота пирамиды. Выбираем длину перпендикуляра таким образом, чтобы боковые ребра не сливались между собой.

Рисунок правильной шестиугольной пирамиды

Поскольку при параллельном проектировании параллельность отрезков сохраняется, основание правильной шестиугольной пирамиды — правильный шестиугольник — изображаем шестиугольником, у которого противолежащие стороны параллельны и равны. Центр правильного шестиугольника — точка пересечения его диагоналей. Чтобы не загромождать рисунок, диагонали не проводим, а находим эту точку приблизительно. Из нее восстанавливаем перпендикуляр — высоту пирамиды — так, чтобы боковые ребра не сливались между собой.

Пирамида – развертка. Развертка пирамиды для склеивания. Развертки из бумаги

Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида – это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.

Материалы и приспособления

Моделирование и выполнение многогранных объемных геометрических фигур – интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:

Определение параметров

Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.

Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.

Как выполняется развертка правильной пирамиды?

Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры.

Сборка макета

Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.

Развертка четырехугольной пирамиды

Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра – треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.

Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.

Завершающий этап выполнения макета

Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.

Объемные макеты сложных фигур

После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.

Построение чертежа

Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями – подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.

Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.

Завершение моделирования

Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.

Изготовление разных моделей многогранников

Выполнение объемных моделей геометрических фигур – увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.

Линейно-конструктивный рисунок пирамиды

Научимся изображать пирамиду в различных положениях.

Изобразите куб в угловой перспективе. Постройте на каждом квадрате основания куба вертикальные и горизонтальные пирамиды.

Рассмотрите пирамиду на рис. 3.43 и ее ортогональные проекции на рис. 3.44. Основанием четырехгранной пирамиды является квадрат, ее боковыми гранями — одинаковые треугольники. Высота пирамиды по отношению к стороне квадрата основания определяет ее пропорции (высокая или приземистая).

Начинать построение стоящей пирамиды необходимо с изображения квадрата основания. Через точку пересечения его диагоналей проведите вертикаль, на которой отложите отрезок, равный высоте пирамиды (рис. 3.45). Соединив полученную таким образом вершину пирамиды с вершинами квадрата основания, получим перспективный рисунок четырехгранной пирамиды (рис. 3.46). Построение пирамиды с вертикальным квадратом основания ведется в той же последовательности.

Сечения пирамиды плоскостями, параллельными основанию, — квадраты, размеры которых зависят от положения секущей плоскости — ближе к вершине пирамиды размер сечений меньше, чем у основания (рис. 3.47). Сечение, перпендикулярное основанию пирамиды, проходящее через ее вершину и среднюю линию квадрата основания, представляет собой треугольник. Все другие сечения пирамиды, параллельные этому — трапеции, большее основание которых равно стороне квадрата основания, меньшее — меняется в зависимости от положения плоскости сечения (рис. 3.48). При построении таких сечений помните, что боковые стороны трапеций параллельны высотам в треугольниках боковых граней.

Линейно-конструктивный рисунок пирамиды Линейно-конструктивный рисунок пирамиды Линейно-конструктивный рисунок пирамиды Линейно-конструктивный рисунок пирамиды Линейно-конструктивный рисунок пирамиды Линейно-конструктивный рисунок пирамиды

Теперь, когда вы хорошо изучили последовательность построения пирамиды и ее сечения плоскостями различного направления, приступайте к выполнению основного задания. Нарисуйте куб (рис. 3.49). Пересеките диагонали всех шести граней куба и проведите прямые, соединяющие центры противолежащих квадратов. Отложите на этих прямых высоты пирамид (рис. 3.50). Все шесть пирамид одинаковы по высоте (1,5а, где а — ребро куба), но на рисунке их высоты имеют разные размеры. Для определения высот пирамид разного положения в качестве единицы измерения используются различные отрезки. Так, например, при определении высот вертикальных пирамид такой единицей измерения является отрезок вертикальной прямой, ограниченный точками центров горизонтальных граней куба. Для высот горизонтальных пирамид такими единицами являются отрезки прямых, проходящие через центр куба и имеющие то же направление, что и определяемая высота. Таким образом, в любом рисунке, основу которого составляют геометрические тела, куб выступает в роли трехмерной линейки, при помощи которой можно определить или измерить длины отрезков, лежащих в трех взаимно перпендикулярных направлениях. Определяя точки вершин пирамид, учитывайте также перспективные сокращения отрезков. Соедините вершины всех шести пирамид с вершинами квадратов оснований (рис. 3.57).

Линейно-конструктивный рисунок пирамиды

Источники:

https://www.uznateshe.ru/risunok-pravilnoy-piramidyi/
https://fb.ru/article/143219/piramida—razvertka-razvertka-piramidyi-dlya-skleivaniya-razvertki-iz-bumagi
https://hspline.com/linejno-konstruktivnyj-risunok-piramidy.html